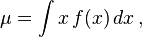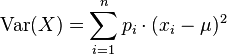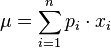Industri asuransi kekurangan tenaga aktuaris. Penggunaan konsultan aktuaris nantinya tidak lagi diperkenankan. Setidaknya diperlukan sekitar 500 tenaga aktuaris hingga 2015. Apriyani Kurniasih
Kelangkaan tenaga aktuaris di industri asuransi mendorong Biro Perasuransian Badan Pengawas Pasar Modal dan Lembaga Keuangan (Bapepam-LK) melakukan penertiban tenaga aktuaris. Fakta di lapangan, jumlah perusahaan asuransi dan tenaga aktuaris belum seimbang. Hal itu mendorong terjadinya bajak-membajak tenaga aktuaris di asuransi. Bahkan, ada pula aktuaris yang dipekerjakan di lebih dari satu perusahaan asuransi.
Mengingat produk dan bisnis asuransi yang terus berkembang, Biro Perasuransian Bapepam- LK kini mewajibkan perusahaan asuransi memiliki tenaga aktuaris sendiri. Dalam rancangan peraturan baru yang disusun Biro Perasuransian Bapepam-LK disebutkan, setiap perusahaan asuransi harus melibatkan komite pengarahan pengembangan produk guna pemasaran produk asuransi, dan salah satu anggota komitenya adalah aktuaris.
Tenaga aktuaris yang dimaksud di sini harus memiliki kemampuan teknis secara matematika, keuangan, dan statistik untuk bisa menganalisis outlook ekonomi ke depan. Lebih jelasnya, tenaga aktuaris dibutuhkan untuk menguatkan perusahaan asuransi dengan kompetensi dan kapasitasnya dalam mengevaluasi risiko yang dihadapi asuransi ke depan.
Mengapa perlu tenaga aktuaris? Bapepam-LK menilai, produk asuransi, termasuk asuransi umum, mulai masuk produk-produk multiyears, yaitu tidak melulu produk setahunan, tapi sudah renewal premium. Artinya, perusahaan asuransi akan menanggung risiko dalam jangka panjang.
Selain itu, karakteristik produknya sendiri ke depan akan berkembang. Untuk itulah, perusahaan asuransi memerlukan kemampuan untuk memprediksi perilaku konsumen dan perilaku ekonomi agar bisa mengetahui kemungkinan default atau kemungkinan klaim beberapa tahun mendatang.
Dalam masa transisi setelah aturan baru tersebut berlaku, regulator masih akan memberikan kesempatan kepada industri untuk mulai membangun tenaga aktuaris di perusahaan masing- masing secara bertahap. Misalnya, dengan melakukan investasi pada human resources-nya untuk dididik menjadi tenaga aktuaris.
Ketika aturan ini diberlakukan dengan masa transisi lima tahun dari sekarang, tidak akan lagi ada tawar-menawar dalam mengimplementasikan aturan tersebut. Atau, perusahaan terancam terkena sanksi.
Data Biro Perasuransian Bapapem-LK menyebutkan, saat ini jumlah tenaga aktuaris yang dimaksud Bapepam-LK baru mencapai sekitar 150. Data Persatuan Aktuaris Indonesia (PAI) juga menyebutkan, dari 350 orang anggotanya, baru sekitar 150 yang berhak menandatangani laporan aktuaria.
Padahal, jumlah yang dibutuhkan sangat banyak. Jumlah tenaga aktuaris nantinya harus disesuaikan dengan kebutuhan tiap perusahaan, misalnya dari jumlah perusahaan asuransi yang ada saat ini, jika satu perusahaan saja membutuhkan dua tenaga aktuaris, idealnya diperlukan sekitar 300-400 orang lagi.
Idealnya, tenaga aktuaris yang dibutuhkan saat ini memang mencapai sekitar 300-400 orang. Namun, melihat perkembangan bisnis asuransi, setidaknya diperlukan tambahan sekitar 200 aktuaris lagi dalam dua hingga tiga ke depan. Artinya, kebutuhan tenaga aktuaris di industri ini bisa mencapai sekitar 500-600 dalam tiga tahun ke depan.
Sumber :http://www.infobanknews.com/2012/05/asuransi-butuh-500-tenaga-aktuaris/














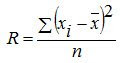
![\operatorname{Var}(X) = \operatorname{E}\left[(X - \mu)^2 \right]. \,](http://upload.wikimedia.org/math/0/b/8/0b8267ff004e01fb5f5ca0da3bd10215.png)
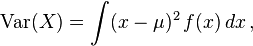
 adalah
adalah